Exploring organizational theory and leadership through the framework of complexity and neural sciences (part 3)
Dear Readers, thank you for your curiosity and valuable comments as well as taking the intellectual and emotional effort to travel the journey together with us. Michel Foucault, late French philosopher and professor at the Collège de France, historian of ideas and social theorist, wrote “people know what they do; frequently they know why they do what they do; but what they don't know is what what they do does.” (Foucault, Madness and Civilization: A History of Insanity in the Age of Reason). In this third blog post around the main theme we’ll continue to explore in the spirit of Foucault and his archaeology of thought; taking deeper analysis regarding the domains, assumptions and things taken for granted regarding scientific management and systems thinking. Shedding light on taken for granted assumptions, shaking the habits and dispelling the familiarity of the accepted unconsidered modes of thought the practices that we accept. We’ll also analyze chaos theory from a mathematical standpoint and reflect for example what does the concept of dependence on initial conditions mean in terms of leadership, traditional view of control and the feasibility of long-term forecasting. Enjoy the next chapter of the journey !

Scientific management began during the industrial revolution with the rise of the factory system, where automation and mass production replaced the handicraft system, where people had worked in small shops or in homes. Industrialization created a need for efficient planning, organizing, influencing and controlling of all work activities. Fredrick W. Taylor is considered the founding father of scientific management. He developed scientific management with the aim of improving efficiency of the organization’s physical activities. At the time it was seen as the best management approach for achieving productivity increases. Taylor argued that the principal objective of management should be to secure the maximum prosperity for the employer, coupled with the maximum prosperity for each employee (Taylor, 1911). He also showed that maximum prosperity can exist only as the result of maximum productivity.
Essentially what Taylor introduced was a sort of guided or standardized way of management based on quantification and scientific research rather than one’s own perception of what was optimum. This heritage is still today highly influential considering management approaches such as Balanced Scorecard, Statistical Process Control and Six Sigma, Lean Management as well as Total Quality Management. This is a form of cybernetic control mechanism whereby feedback loops the target is to return to the state of equilibrium. This approach emphasized on the use of empirical research for developing a comprehensive management solution. Taylor believed that by carefully observing the day to day activities of workers in the organization, management could identify bottlenecks (see also the Theory of Constraints) as well as redundant processes and find solutions on how to solve and eliminate these problems. This principle is perhaps one of the most important contributions of Taylor: the idea that managerial decision making can be done following a scientific approach (Locke, 1982). Taylor suggested that managers carefully study each and every task or process involved in production of a single item and use the information gathered to divide the process into simple steps and determine how each task should be accomplished. By using the time and motion studies managers would be able to determine the exact time and skills needed for each task enabling them to standardize the work.
Knowingly or unknowingly, Taylor made very strong assumptions about human mind and behaviour. His entire work was based upon the assumption that human beings were like machines and that they would do exactly what they are told to do without any uncertainty related to attitudes, motivational factors or emotional factors. During the time that Taylor developed the principles of scientific management, the behaviourism school of psychology was the dominant school of thought used to understand human psychology and the alignment is very clear. John Watson, the American psychologist who introduced behaviourism, insisted that behaviour is a simply a physiological reaction to environmental stimuli i.e. human behaviours are acquired or learned through interaction with one’s environment. Watson did not believe in human instinct, thought or emotion. Instead, he concluded that human behaviour is strictly shaped by one’s environment. Watson also claimed that psychology was not concerned with the mind or with human consciousness but it was concerned only with behaviour (Watson, 1924). As already introduced, behaviourism is based on the idea that human behaviour is made up of observable and measurable responses to the environment. Furthermore, this behaviour can be shaped or controlled through a process known as conditioning. There were two main methods of conditioning proposed; the first was classical conditioning in which behaviour is learnt through association. This is a type of learning in which a stimulus acquires the capacity to evoke a reflexive response that was originally evoked by a different stimulus. As we come to see, the principles of scientific management and the underlying intellectual domain are highly similar to the ideas of behaviourism. An organization is split to the smallest possible unit, very strict tasks and procedures are defined for each worker, they are then trained on how to carry out these tasks effectively, and to every unit that is successfully processed, associated rewards are given. It's clear that what underlies this framework is the Kantian split between the leader as an objective observer following rationalist teleology, and the followers bound by the forces of efficient causality.

Systems theory is the interdisciplinary study of systems whereas a system is a conglomeration of interrelated and interdependent parts which can be natural (i.e. cell or an organism) or human-made. System is simply the name given to an object studied in some field and might be abstract or concrete; elementary or composite; linear or nonlinear; simple or complicated; complex or chaotic. Systems theory attempts to describe and understand the common structure, attributes and emergent properties of all types of systems - physical, biological and social - by viewing them as systems rather than as objects or isolated entities (Bertalanffy 1956).

Throughout the systems thinking the engineering sciences entered the domain of biological and social realms. Every system is bounded by space and time, influenced by its environment, defined by its structure and purpose, and expressed through its functioning. A system may be more than the sum of its parts if it expresses synergy or emergent behaviour. Ludwig von Bertalanffy and other pioneers such as Churchman (1968, 1979) were the first ones to challenge the underlying assumptions made by this reductionism method which assumed that a system could be broken down into its individual components, so that each component could be analysed as an independent entity, and the components could be added in a linear fashion to describe the totality of the system. Von Bertalanffy instead proposed that a system is characterized by the interactions of its components and the nonlinearity of those interactions (Bertalanffy 1969)

Formulas that describe the motion of viscous fluid substances: Navier–Stokes equations
The dynamics of a system describes the manner in which the system changes. A system is deterministic (fixed or periodic pattern) if it is possible to uniquely determine its past and future trajectories (i.e. all points it passed through and will pass through) from its initial state. In this way, the system obeys deterministic laws. The behavior of a chaotic system appears random, but is generated by simple, non‐random, deterministic processes: the complexity is in the dynamical evolution (the way the system changes over time driven by numerous iterations of some very simple rule), rather than the system itself. Chaotic behavior pattern is generated by feeding solutions back into the rule as a new initial condition. This aperiodic behavior is not complex in the sense of complex systems science, but rather it is chaotic in a very precise mathematical sense. The interactions between the subunits of a complex system determine (or generate) properties in the unit system that cannot be reduced to the subunits (and that cannot be readily deduced from the subunits and their interactions). Such properties are known as emergent properties. Complex systems often exhibit self‐organization, which happens when agents spontaneously reorganize themselves (generally in an optimal or more stable way) without “external” tuning of a control parameter. This notion is very different from cybernetic control mechanisms embedded in equilibrium dynamics.

To understand the linear, chaotic and complex behavior of a system it’s helpful to examine thermodynamics and fluid mechanics. Thermodynamics is the study of heat and thermal energy, whereas fluid mechanics studies fluid behavior and is concerned with the response of fluids to forces exerted upon them. The 1st law of thermodynamics states that that energy cannot be created or destroyed, or the total quantity of energy in the universe stays the same. The 2nd law of thermodynamics states that the state of entropy of the entire universe, as an isolated system, will always increase over time. This means that the system's disorder (or the number of potential states of the system) increases over time. Now considering fluid flowing through a channel, we may understand that besides the qualities of the fluid (i.e. viscosity) and the channel structure (such as hydraulic diameter) also the fluid velocity influences the type of flow pattern. Reynolds number (ReN) quantifies how much the flow is affected by inertia and the ratio of the inertial forces to the viscous forces. The viscous forces are the forces due to the friction between the layers of the fluids. Numerator defines inertial forces and the denominator defines viscous forces. Analyzing the flow regimes, fluid flow is considered laminar at low flow velocities, but begins to turn into turbulence as the velocity increases beyond the critical value. Transitional region exists both directions, the laminar–turbulent transitional or turbulent–laminar transitional flow. Transition from laminar to turbulent occurs within a range of velocities, where the flow fluctuates between laminar and turbulent flows, before becoming fully turbulent. Within this transitional flow region, the behavior of the fluid flow demonstrates bounded instability which engenders a constant dynamic interplay between order and disorder. The phrase ‘edge of chaos’ was coined by mathematician Doyne Farmer to describe the transition phenomenon. It has since been studied further as part of dissipative systems (Prigogine et Al.) far from equilibrium and as part of complexity research in general.
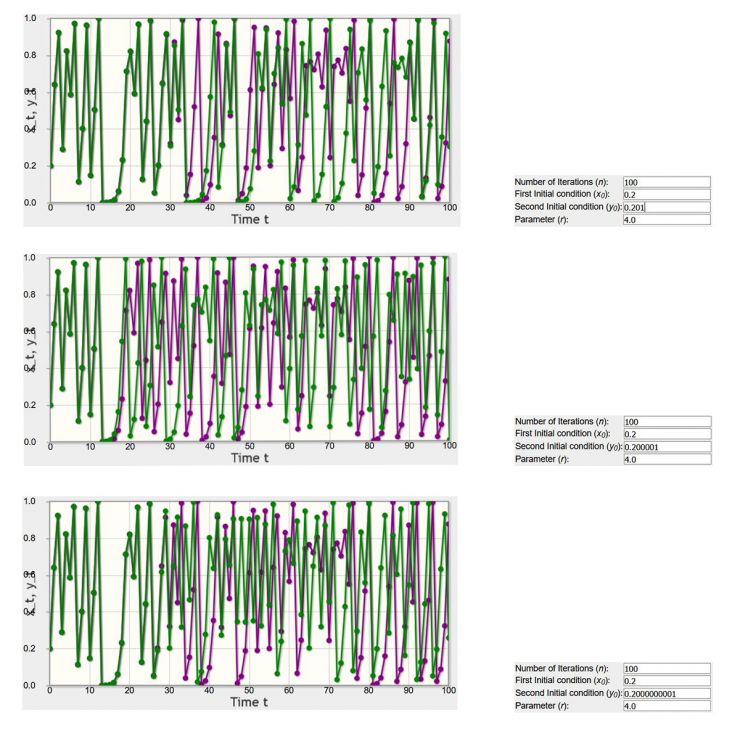
Time series plots for the logistic equation f(x)=rx(1-x) for two different initial conditions
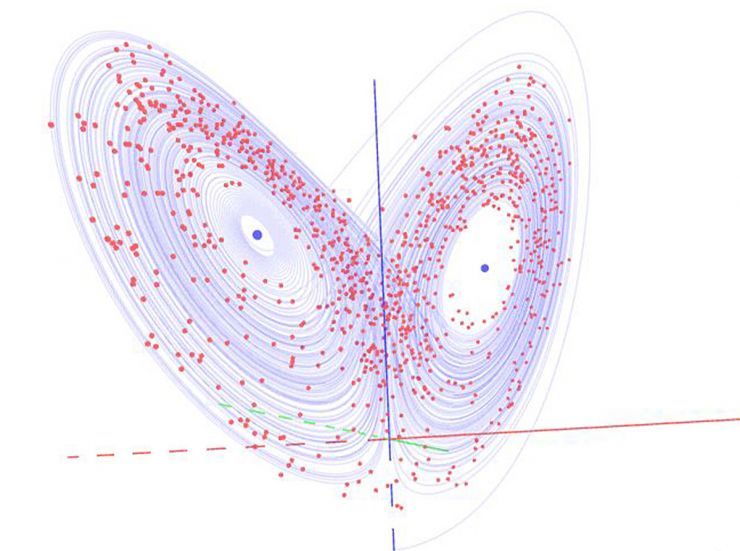
The Lorenz attractor is a set of chaotic solutions of the Lorenz system
At the heart of chaos is the notion of initial value sensitivity which sets limits to the horizon of predictability. This is system level unpredictability even if the system is deterministic. This is caused by two issues: first of all, identification of all variables influencing the dynamics of a given system is difficult (i.e. variables considered in weather modeling) and secondly, the finite accuracy of arithmetic’s (i.e. how many decimals are considered in input values). Lorenz’s famous system of three variables showed that when tiny measurement errors enter into iterative calculations, this minor difference amplifies over time growing exponentially, eventually degrading the prediction accuracy. From a mathematical standpoint this means that if we follow the time evolution of two or more initially close-by trajectories, we’ll recognize gradually intensifying divergence with these trajectories. It’s very important to understand that despite the limitations of the forecasting horizon due to the number of agents and their sensitivity to the initial conditions, chaos theory remains deterministic. With the hypothetical perfect knowledge of the initial conditions and infinite computing power, the course of this action of a system can be predicted in chaos theory. Now let’s draw some analogies to human behavior and social sciences by reflecting the wealth of context-specific factors influencing organizational behavior (beliefs, motives, conflicts, capabilities, etc.). How feasible and realistic we see a specific strategy, which has been proven successful in particular social, historical and cultural context and environment, to generate similar outcomes when applied to a new contextual situation? How about the usefulness of mid-to-long term planning, i.e. 5-10 years strategic horizons? More detailed analogies between the chaos theory and human action shouldn’t be drawn. This is due to the fact that it’s clear that human interaction does not create a system and human agents change their behavior through learning which means this process does not follow deterministic laws.
Besides the initial value sensitivity, another important part of chaos theory are fractals. A fractal is a repetitive pattern that is self-similar regardless of the proximity of space and time. The most well-known fractal is probably Mandelbrot’s set based on iteration of a simple expression. Another classic example of fractals is the Sierpinski triangle, which is formed by dividing the triangle into four parts, removing the middle one, and repeating the process for the remaining parts. Fractals impact way beyond mathematics and as an example our lung geometry is fractal or self-similar. Our body fine-tunes each of its divisions precisely into sections so that each section is a smaller version of the previous one. This ‘modular design’ makes the lungs perform the diffusion of oxygen from the inhaled air at any size. Also, a healthy heart beat embodies a predictably unpredictable fractal pattern as time series.
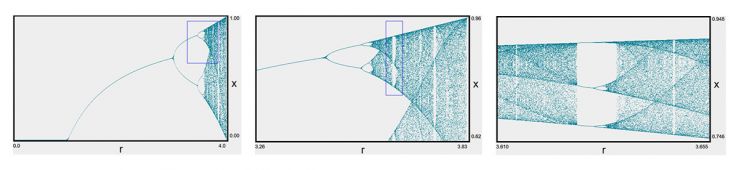
Bifurcation Diagram for the Logistic Map: xn+1= r xn (1-xn)
Systems often demonstrate dynamic behaviour and over time they tend to adapt to the changing environment that they are part of. Negative feedback simply means that the outcome of a previous action is compared with some desired outcome and the difference between the two is fed back as information that guides the next action in such a way that the difference is reduced until it disappears (Stacey et al 2007). Negative feedback can also be described as a process of transmitting information about any divergence of behaviour in the system that is different from a predefined goal and corrective action is taken, on the basis of this information, to bring the behaviour back towards the goal. The aim of negative feedback is to sustain the system in a state of equilibrium or in other words control the system. A commonly quoted example of this kind of control system is the domestic central heating system. A domestic central heating system consists of a heating appliance which is fixed with a regulator. The regulator contains a sensor, which senses the temperature in a given room and turns the heating appliance on and off depending on the desired temperature. It is important to remember that this desired temperature is predefined by an observer who is not part of the system. When the room temperature falls below the desired temperature the regulator detects this difference between the actual and desired temperature and responds to this negative feedback by turning on the heating appliance. If the systems heat above the desired temperature level then the regulator will switch it off, thus keeping the room temperature at a stable level over time (Stacey et al., 2007).
In organizational systems control and feedback (whether positive or negative) is a highly important concept. According to Ralph Stacey there are two main forces that drive an organization over time. The first force is the drive to achieve some purpose: from this perspective the organizations are seen as goal seeking systems and their goals drive their actions (Stacey et al., 2007). For example, the driving factor for an organization can be its goal to be the best in a particular technology or industry. The second force comes from the external environment which is connected to the organization through feedback channels. From this perspective organizations are self – regulating systems that adapt to the changes in the environment in which they are a part of.
The Mandelbrot set as an example of a complex structure arising from the application of simple rules

An important derivative of systems theory to organizational theory and management has been systems’ thinking. Systems’ thinking is a way for teams and individuals to look for changes that will give long-term improvements rather than the quick fix that eventually fails but is reapplied over and over (Senge, 1990). This theory indicates that organizations that work from within the systems framework begin by looking for the connections between the various parts of the system to ensure better coordination of organizational functions. Systems’ thinking also attempts to integrate the various parts of a system in a way that optimizes, rather than maximizes, the performance of each of its parts in order to achieve organizational effectiveness. This holistic approach recognizes that relationships and the context in which they function are just as important as the details. There’re further derivatives of systems´ thinking such as Systems Intelligence developed at Helsinki Aalto University Systems Intelligence Research Group by Professors Esa Saarinen and Raimo P. Hämäläinen. By Systems Intelligence they mean intelligent behaviour in the context of complex systems involving interaction and feedback. A subject acting with systems intelligence engages successfully and productively with the holistic feedback mechanisms of her environment. She perceives herself as part of the whole, the influence of the whole upon herself as well as her own influence upon the whole. Observing her own interdependency with the feedback-intensive environment, she is able to act intelligently (Esa Saarinen and Raimo P. Hämäläinen, 2004).
Today, the open-system approach (a system in exchange of matter with its environment), serves as a model for business activities in a number of industries. The primary activity of any business is transforming inputs to outputs. Companies use inputs such as labour, funds, equipment, and materials from the external environment to produce goods or to provide services which are released back into that same environment. The company is divided into subsystems or departments such as production, marketing, research which are all working together to produce the required outputs. The production subsystem, for example, focuses on converting inputs into marketable outputs and often constitutes a primary purpose of a company. The boundary of this particular subsystem's goal is to obtain inputs or resources, such as employees, materials, equipment, and so forth, from the environment outside of the company, which are necessary for the production of product x,y and/or z. At the same time the management subsystem, supervises and coordinates the other subsystems to ensure that each subsystem functions efficiently. The management subsystem uses inputs such as information both from the organization’s internal operations and the external environment to make decisions, resolve conflicts, solve problems, allocate resources, and so on. Both subsystems interact with one another and at the same time interact with the external environment.
Organizations are also considered to be open systems which exist by importing energy/materials from its environment across a boundary, transforming them and then exporting them back across the boundary. (Stacey et al., 2007) The boundary region between the organization and the environment is seen as protecting the organization but at the same time a point at which mediating or regulating activities can take place. In organizations regulatory functions are performed by leaders/managers and therefore it is interesting to note that in the systems’ thinking perspective the organization’s management is actually not seen as part of the system. In fact, they act as external observers who observe the system, make all the major decisions and inject change into it, very similar to the scientist in scientific management. Systems thinking is a very powerful tool to analyse and explain the interconnections and the dynamics related to issues such as climate change, however when applied to leadership and organizational theory it very clearly contains the problematic split between rationalist/formative teleology.
As a summary of the 3:rd chapter:
- A dynamical system is a system that evolves in time according to well-defined and unchanging rules. A dynamical system has sensitive dependence on initial conditions if arbitrarily small differences in initial conditions eventually lead to arbitrarily large differences in the orbits. This is also known as the Butterfly effect. For any initial condition there is another initial condition very near to it that eventually ends up far away. To predict the behavior of a system requires knowing the initial condition with impossible accuracy.
- A dynamical system is chaotic if: the dynamical system is deterministic and it’s orbits are bounded. The system’s orbits are aperiodic and the system has sensitive dependence on initial conditions. Bifurcation demonstrates the period doubling route to chaos is observed in physical systems. Chaotic trajectories in phase space often get pulled to strange attractors.
- “If we knew exactly the laws of nature and the situation of the universe at the initial moment, we could predict exactly the situation of that same universe at a succeeding moment. but even if it were the case that the natural laws had no longer any secret for us, we could still only know the initial situation approximately. If that enabled us to predict the succeeding situation with the same approximation, that is all we require, and we should say that the phenomenon had been predicted, that it is governed by laws. But it is not always so; it may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible...” (Henri Poincaré, 1854-1912)
- Dynamics gives us a vocabulary for describing complex behavior. What we see is complex and unpredictable behavior from simple, deterministic rules. Humans as agents change their ideologies, values and preferences, their decision making is biased, and the interaction dynamics evolve over time. This is non-deterministic behavior pattern and this trajectory leads to fundamental limits to detailed prediction, which is very far away from the notion of control and the way we invest and discuss strategic planning (mid-to-long term horizon).
BlackSmith Consulting Oy, Juho Partanen
Chairman of the Board
+358 40 153 5606
juho.partanen@blacksmithconsulting.fi


